
As I was working on my last game, GlideWords, it struck me that the recent “Daily Puzzle” craze has really been focused on word games, leaving math nerds with few options to compete. Looking further back, even common number puzzles like 2048, griddlers, or traditional sudoku are more about patterns than actual math.
and so, an idea slowly formed, that would become PrimalPairs.
The idea behind PrimalPairs is simple. You are given a large prime number, a current total, which starts at zero, and a series of small prime operands. Each operand can be added to, subtracted from, multiplied with or divided from the current total, to change its value. The goal is to make the current total match the large prime in as few moves as possible.
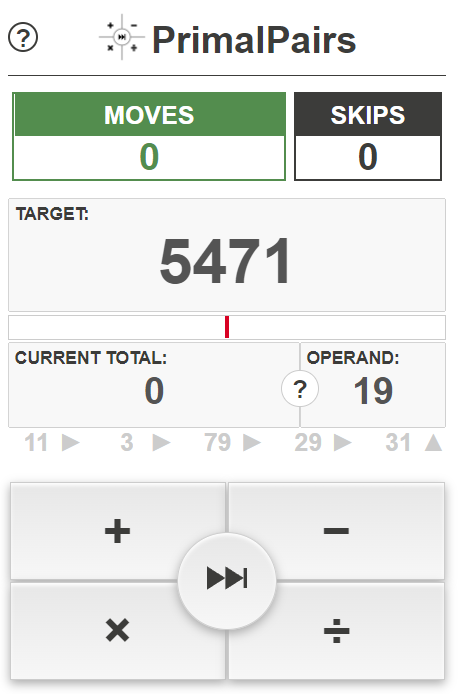
A few more things to know
- You can skip an operand, if you want, but it will still cost you a move.
- The current total is not allowed to go negative. It will be reset at zero if an operation would result in a negative number.
- All division is rounded down to the nearest integer.
- below the current total and operand, there is a list of upcoming operands. Use this list to strategize each move.
Tips for playing like a pro
- Most perfect games are 7 to 9 moves long.
This means that you normally cannot fully solve the game from the information on screen at the start. You must think about your strategy in stages, and reassess with each new move. You are very unlikely to get a perfect game on your first playthrough of the day, so I recommend taking note of the sequence of primes that appear in your first playthrough, to inform your next attempt. - Your first move should almost always be addition.
Since the initial total is zero, any operation but addition is equivalent to skipping the first number. It is almost always better to get to a total that other operations can impact, than to skip and stay limited to addition. - Your last move will never be multiplication or skipping.
Since your target is always a prime number, you will never reach it by multiplying your total by your operand. - Division is the most powerful late-game move.
Because all division is rounded down, it can be used to solve issues of being just a few numbers off. For example, if your target number was 5, and you worked backwards to try to make your last move dividing by 11, your next to the last total could be anything from 55 to 65, and the result would still be the same. This means that often the optimal solution will have division as one of the last few moves. - Multiplication is the most powerful early game move.
Because the goal is to grow your total quickly to reach or surpass the target number, the early game must involve multiplication, although, in some cases a sequence of addition may be used first to prepare the total for a specific operand. - Your second move is the most strategic.
Since the first move can be made almost without consideration, your second move contains seven unique primes to strategize with. This is the time to stop and develop a strategy for how to handle each operand, as it appears. Future moves should involve reassessing and tweaking this plan, but by move 3 or 4, the rest of the game may be on auto-pilot. - You have to play to get good.
It is very unlikely (unless your name is Rachel Riley) that your day-job involves solving puzzles like this. Practicing will improve both your intuition and your overall speed at strategizing.